1. Motivation
The recent rapid advance in high power femtosecond laser technology has attracted researchers to the generation of ultra-intense, relativistic laser field, the study of the interaction physics of such a intense laser with matters, and possible applications of related phenomena in various sciences and technologies. In this context, the radiation characteristics of relativistic nonlinear Thomson scattering (RNTS) has been investigated for various applications in science and technology.

2. Result

The paraxial approximation to a laser field is no longer valid if the beam waist of the laser is in the order of its wavelength. In such a case, a laser beam propagating even in a free space is not purely transverse but contains the significant longitudinal field. The investigation reveals that Thomson scattering characteristics by a relativistic electron (80MeV) of a tightly-focused, co-propagating laser field is sensitive to the electron¡¯s initial transverse position and phase with respect to the laser field: the electron radiates more strongly when it is initially located off-laser axis by about the beam waist than when on-laser axis. The enhancement of about 2000 in the radiation power is noticed for the focused (beam waist of 5 ¥ìm) laser intensity of 1 x 1018 W/cm2 compared to a paraxial Gaussian beam case.

Fig. 1. Schematic diagram of the interaction geometry between an electron and a co-propagating laser pulse. The black and white dot illustrate the electrons which propagate to z = 0 and when the laser pulse is absent, respectively.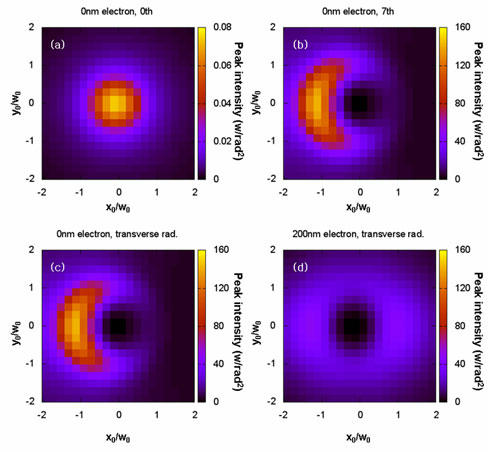

Fig. 2. Peaks of the angular radiation powers with respect to initial positions (x0, y0) for the z=0nm and 200 nm electron, showing the initial positions (x0, y0) of the z=0nm and 200 nm electron favorable to strong radiation. (a) In the case of the paraxial approximation, that is, only the 0th-order field in is considered. (b) In the case of non-paraxial approximation where high-order fields up to are considered. (c) the same as in (b) but only a transverse acceleration is considered. Note that the intensity is about the same as in (b). (d) the same as in (c) but for the z=200 nm electron.

3. References

[1] International conference on ultrahigh intensity lasers development, science and emerging applications, Cassis, France, Sept 25-29, 2006.
[2] E. Esarey et al, Phys. Rev. E 48, 3003 (1993).
[3] F. V. Hartemann and A. K. Kerman, Phys. Rev. Lett. 76, 624 (1996).
[4] Y. Ueshima, et al., Laser and Particle Beams 17, 45 (1999).
[5] K. Lee, et al., Opt. Express 11, 309 (2003).
[6] F. V. Hartemann, et al., Phys. Rev. E 72, 026502 (2005).
[7] J. Koga, et al., Phys. Plasmas 12, 093106 (2005).
[8] K. Lee, et al., Phys. Plasmas 12, 043107 (2005).
[9] S.-W. Bahk et al. ¡°Generation and characterization of the highest laser intensities (1022 W/cm2),¡± Optics Letters, 29, 2837 (2004)
[10] L. W. Davis et al., ¡°Theory of electromagnetic beams¡±, Phys. Rev. A 19, 3 (1979)
[11] J. P. Barton et al., ¡°Fifth-order corrected electromagnetic field components for a fundamental Gaussian beam¡±, J. Appl. Phys. 66, 7 (1989)
[12] Y. I. Salamin, Appl. Phys. B 86, 319-326 (2007).
[13] Y. I. Salamin and C. H. Keitel, Phys. Rev. Lett. 88, 095005 (2002).
[14] S. Huang, et al., Physics of Plasmas 14, 123107 (2007).
[15] X. He, et al., Physics of Plasmas 12, 073101 (2005).
[16] B. Xie, Appl. Physics Lett. 91, 011118 (2007).